Introduction| Task|Process| Resources| Evaluation| Conclusion| Teacher Notes| Additional Comments

INTRODUCTION

Students who take the GED exam almost always take one of the tests last. Do you know which one it is? It’s math. Why does math seem so hard? I think it’s because students have not learned  strategies for solving problems. To them math looks like a bunch of numbers with no purpose. Would it be easier to solve problems if you knew different ways to take the problems apart?

TASK

During this Webquest you will be introduced to nine different strategies for solving math problems. It will be your job to review the sample problems given, find another problem that uses the same strategy and then enter the new problem to the class book.

PROCESS

1. Review the nine strategies presented below for solving math problems. Read each strategy carefully and follow the sample problem.

2. Analyze the strategies. Which ones were new to you? Which ones have you already used?

3. Did you understand each strategy? If not, consult another person in the class who could help you understand, and reread strategy.

4. When you understand all the strategies, find an example problem for seven of the nine strategies. It is your choice. Record your response in your class notebook.

5. Your problems will be evaluated according to the rubric at the end of this exercise.

6. You do not need to complete all of the exercises at one time. It is more important to learn each of them well, so take your time.

_________________________________
THE NINE STRATEGIES

1. Make a model

Make a model or representation using the data given in the problem.

Problem – Rachel had 28 blocks. If she stacked them in rows starting with seven blocks and subtracted one block from each new row, how many rows would she need to use all the blocks?

Using the model Rachel would need seven rows.

2. Use smaller numbers

Using smaller numbers can make the problem easier to imagine and then solve.

Problem – Jose lives 3000 miles away from his family. If you drive 600 miles a day, can you estimate how many days it will take into drive?

3000 total miles
600 miles per day

Cross out the extra zeroes making sure you cross out the same number of zeros from the numerator as the denominator.

300 total miles
6 miles per day = 5 days

It will take Jose five days to drive to his family’s house.

3. Use a graph

A graph is another way of picturing a problem so it can be solved. Graphs have two dimensions; the X axis is horizontal and the Y axis is vertical.

Problem –Adrienne took a typing class to improve for speed on the computer. Each week she improved by 15 more words per minute. How many weeks will it be before she can type 80  words per minute?



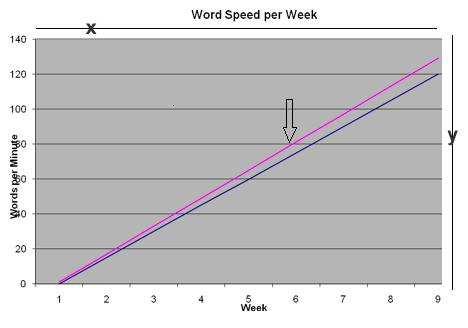
At the end of six weeks she will be able to type 80 words per minute.

4. Draw a picture

Students often get stuck when they try to solve problem before they understand it. Trying to picture helps you visualize the problem and makes it easier to solve.

Problem – Casey had six cats. Two of the cats had litters of three cats each. She gave away four of those kittens. How many cats and kittens were still left after she gave away the kittens?

Count the number of cats in the pictures. Then subtract four. How many cats are left?

Casey still had 8 cats! Here kitty kitty!

5. Use graph paper to trace a route

Graph paper can be used to solve problems especially those involving directions.

Problem – Graham went for a walk one day. He started at the corner of Harrison & 2nd. First he walked five blocks north, then three blocks east and then four blocks south. He got tired and called a sister for ride. She asked him where he was. What is the name of the intersection where Graham stopped?
 

          

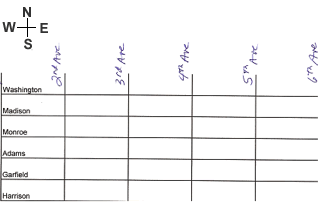
Graham was at the intersection of Garfield and 4th.

6. Look for a pattern

Patterns are everywhere. When you see a pattern in math, you can then predict what is coming next.

Problem – James runs every week. He adds 2 miles to his weekly run each week. If he ran 3 miles the first week, how far did he run in week eight?
 

In the eighth week James ran 17 miles.

7. Make an organized list

Another way to solve a problem is to list all the parts in an organized way and then cross up the duplicates.

Problem – There are five flavors of ice cream. How many different combinations of cones can be made if each column has two different scoops?

The flavors are:
V = vanilla C = chocolate
S = strawberry B = banana
R = raspberry
 

To solve the problem list every possible combination of two scoops, then cross out the duplicates. The x in a square represents combinations that are the same ice cream flavor.

There are 10 possible combinations.

8. Work backwards

When working backwards is the strategy, start with the facts at the end of the problem and work backed work the beginning.

Problem – Charlie had some pennies. He had six more than Rosie and Rosie had five more than Harry. Harry had four pennies. How many pennies does Charlie have?

When solving the problem, start with the information you know. The first thing you know in this problem is that Harry had 4 pennies. The next thing you know is that Rosie had five more than Harry so 5 would be added to Harry’s 4. Continue on with the problem by adding the number of pennies Charlie has to the number Rosie has.

Charlie has 15 pennies.

9. Guess and check

Guess and check is exactly what it sounds like. You guess a number, plug it into the problem and see if it works. If not, guess again.

George took a $20.00 bill to grocery store. He bought the following items:

Bread $2.87
Milk $3.39
Hamburger $4.55
Chili beans $1.79
Licorice $2.50
Deodorant $5.55

Does George have enough money to pay his bill? I guess that he does.

By rounding the numbers we can get a better idea if he has enough money.

Bread $3.00
Milk $3.00
Hamburger $5.00
Chili beans $2.00
Licorice $3.00
Deodorant $6.00

The total of all the estimates is $21.00.

Since George still has to pay sales tax after purchasing the items, he will not have enough money. (George better put the deodorant back).

RESOURCES

The following resources are available to you.

Steck-Vaughn GED study guide
GED math practice books
Newspapers
Magazines
Life experience stories (make it up)
Interview with a neighbor or friend
GED web sites –
www.mathacademy.com/pr/prime/articles/storprob/index.asp
www.ket.org/ged2002/math/mathlesson14a.htm
www.aaamath.com/b/est.htm
www. Mcdonaldpublishingcatalog.com/solving_word_ _problems_smart_bookmarks_-p-128775.html  

Evaluation Rubric

CONCLUSION

Congratulations! You’ve just reviewed nine different strategies for solving math problems and you’ve contributed seven new problems. By studying these approaches you’re much better prepared to take the GED exam and pass. In addition, you’ve helped others prepare for the exam. Good for you!

TEACHER NOTES

During this exercise I’ve tried to take the bugaboo out of math. The strategies are presented with simple problems. The focus is on the student understanding how the strategy works.

In my classes I always offer students a choice. I’ve found that students are more motivated by choices and frequently will complete all of the work. For adults with busy lives completing less than 100% of the problems gives them a break.

The reading level of these exercises is 5.6 grade equivalents on the Kincaid scale. Because of this, these exercises are also appropriate for pre-GED students.

Additional Comments

This Webquest was designed for my students at the jail who do not have access to computers. Although references are given for web sites, they would not be able to use them.

Fairy tales are an important part of our culture and can be confusing to ESL students. References are constantly made such as, “she’s waiting for her prince charming,” or “here comes the big bad wolf”. One of the variations for this exercise could be to rewrite the problems using different fairy tales as a source of information. Students could collaborate in groups to study culture as well as math.